Zcash’s next major protocol upgrade, codenamed Sapling, will feature a number of improvements to the performance, security and usability of our shielded transactions. This is the first in a series of blog posts that will explore progress made in Sapling’s development.
BLS12-381: a new zk-SNARK curve
Zcash’s zk-SNARKs currently rely on a pairing-friendly Barreto-Naehrig elliptic curve construction implemented inside of libsnark, which was designed by our scientists many years ago. In the time since, Kim–Barbulescu’s optimization to the number field sieve algorithm reduced the conjectured security level of this curve to around 110 bits, though the curve’s concrete security given current research still remains around 128-bits as originally intended.
As an extra precaution, we’re taking the opportunity to upgrade our elliptic curve in the Sapling upgrade. Earlier this year, I presented a new curve called BLS12-381. This curve targets 128-bit security using more conservative recommendations suggested by several recent papers.
There is now a Rust-language implementation of this curve. It comes with strong memory-safety guarantees as it does not use any unsafe{} code or assembly optimizations. Despite being a larger curve, this new implementation is more efficient than the implementation of BN254 that we currently use in Zcash.
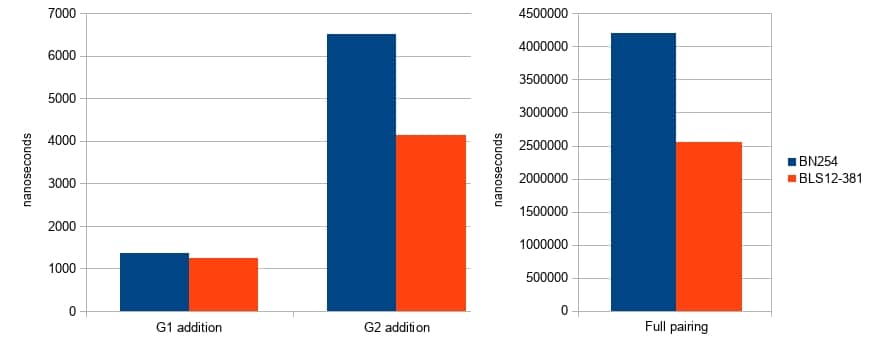
The speedups are especially pronounced in pairing and :math:`mathbb{G}_2` arithmetic, which increases the performance of zk-SNARK proving and verification.
New multi-exponentiation algorithm
The most expensive part of creating a zk-SNARK proof is the evaluation of large polynomials over the elliptic curve groups :math:`mathbb{G}_1` and :math:`mathbb{G}_2`. This is done with a so-called “multi-exponentiation” algorithm that computes :math:`prod_{i=0}^{n}{b_{i}^{s_i}}` for some large number of exponents :math:`vec{s}` which reside in memory, and a large number of bases :math:`vec{b}` which reside on disk inside the zk-SNARK proving key.
Currently, we use libsnark’s implementation of the Bos-Coster algorithm. In the worst case, this algorithm uses as much memory as the number of bases being operated on, and so the only avenue for decreasing memory usage is working with smaller subsets of the bases at a time. As an example, Ariel Gabizon implemented this kind of an optimization in a change to libsnark.
libsnark has recently implemented a variant of Pippenger’s algorithm which splits the multi-exponentiation into bitwise regions of the exponent, accumulating bases into buckets and performing summation by parts. This algorithm is not only more efficient than Bos-Coster, but is very convenient in the context of streamed proving. With this algorithm, we can avoid loading the proving key into memory before constructing a proof, which is a primary source of memory usage in our system.
New proving system
Of course, performing fewer multi-exponentiations would also be a nice way to improve runtime performance. We are strongly considering the use of a new zk-SNARK proving system, discovered by Jens Groth, to replace PGHR (Pinnochio). This proving system makes stronger cryptographic assumptions, but has smaller proofs and faster proving/verification.
What’s more, Groth’s new proving system allows us to design cheaper multi-party computations and other really interesting features that we’ll talk about more in a future blog post.
Next steps
Although the above efforts combined offer substantial improvements to memory usage and proving time, reducing the size of our zk-SNARK circuit will have a much more noticeable effect. We have built a number of new crytographic primitives on top of the BLS12-381 construction which allow us to shrink the size of our arithmetic circuits, reduce the size of Zcash addresses, and simplify the protocol.
In our next blog post, we’ll talk more about these primitives and how much all of these improvements will help performance of our zk-SNARKs.